Wow, I finally managed to pass the exam of DBT Developer certification. I failed two times first because I didn't had much of handson experience with DBT. That will change in the future. So, I had to learn everything from the documentation and from a lot of Udemy tests. Although the tests available on the internet doesn't completely cover the questions on the real exam of DBT, it helped a lot to understand DBT. I did that by researching the answers, googling and reading the documentation of DBT. Last but not least I practiced a bit with DBT on a small mock-up project that I've created.
BI Future Blog
Data, Data modeling, Data warehouse, Business Intelligence & Analytics
vrijdag 16 februari 2024
Certified DBT Developer certification
zaterdag 30 december 2023
Ephemeral tables in DBT (Part XI)
Introduction
In this blogpost we're going to take a look at a specific type of a materialization, known as ephemeral. According to DBT : materializations are strategies for persisting dbt models in a warehouse. There are five types of materializations built into dbt. They are:
- table
- view
- incremental
- ephemeral
- materialized view
This blogpost is a blogpost in a serie of blogposts :
- Build a data warehouse with DBT and Snowflake on AdventureWorksLT (PART I)
- Build Staging and Dimensions in DBT for Snowflake (PART II)
- Sources in DBT for Snowflake (PART III)
- Data freshness for DBT in snowflake (Part IV)
- Snapshots in DBT for Snowflake (Part V)
- Generic tests in DBT for Snowflake (PART VI)
- Singular tests in DBT for Snowflake (Part VII)
- Add packages to your DBT project (Part VIII)
- Adding documentation to your DBT project (Part IX)
- Working with hooks in DBT (Part X)
- Ephemeral tables in DBT (Part XI)
Ephemeral example
Final thoughts
vrijdag 29 december 2023
dbt Analytics Engineering Certification Exam cheatsheet
Introduction
I'm preparing for the DBT exam and I used the "dbt Analytics Engineering Certification Exam Study Guide" for searching for more information about the topics covered in the exam. I stored the links that I used in this blogpost, just helping you too. I hope you enjoy it.
I'll frequently update this blogpost. I just started with a couple of topics.
Topic 1: Developing dbt models
- Identifying and verifying any raw object dependencies
- Understanding core dbt materializations
- Conceptualizing modularity and how to incorporate DRY principles
- Converting business logic into performant SQL queries
- Business logic in DBT
- Refactoring legacy SQL to dbt
- How dbt Can Help Solve 4 Common Data Engineering Pain Points
- Using commands such as run, test, docs and seed
- Creating a logical flow of models and building clean DAGs
- Data modeling techniques for more modularity
- How we structure our dbt projects
- dbt DAG: Definition, Usage, and Examples
- Defining configurations in dbt_project.yml
- Configuring sources in dbt
- Using dbt Packages
Topic 2: Debugging data modeling errors
- Understanding logged error messages
- Troubleshooting using compiled code
- Troubleshooting .yml compilation errors
- Distinguishing between a pure SQL and a dbt issue that presents itself as a SQL issue
- Developing and implementing a fix and testing it prior to merging
Topic 3: Monitoring data pipelines
- Understanding and testing the warehouse-level implications of a model run failing at different points in the DAG
- Understanding the general landscape of tooling
Topic 4: Implementing dbt tests
- Using generic, singular and custom tests on a wide variety of models and sources
- Understanding assumptions specific to the datasets being generated in models and to the raw data in the warehouse
- Implementing various testing steps in the workflow.
- Ensuring data is being piped into the warehouse and validating accuracy against baselines
Topic 5: Deploying dbt jobs
- Understanding the differences between deployment and development environments
- Configuring development and deployment environments
- Configuring the appropriate tasks, settings and triggers for the job
- Understanding how a dbt job utilizes an environment in order to build database objects and artifacts
- Using dbt commands to execute specific models
Topic 6: Creating and Maintaining dbt documentation
- Updating dbt docs
- Implementing source, table, and column descriptions in .yml files
- Using dbt commands to generate a documentation site
- Using macros to show model and data lineage on the DAG
Topic 7: Promoting code through version control
- Understanding concepts and working with Git branches and functionalities
- Creating clean commits and pull requests
- Merging code to the main branch
Topic 8: Establishing environments in data warehouse for dbt
- Understanding environment’s connections
- Understanding the differences between production data, development data, and raw data
Working with hooks in DBT (Part X)
Introduction
In one of my projects I've built a logging mechanism with stored procedures in Snowflake. It will log the start of a run, the start of load procedure, the end of the load procedure and the end of the run. You can do this also with hooks in DBT.
From DBT docs : Hooks are snippets of SQL that are executed at different times:
- pre-hook: executed before a model, seed or snapshot is built.
- post-hook: executed after a model, seed or snapshot is built.
- on-run-start: executed at the start of dbt build, dbt compile, dbt docs generate, dbt run, dbt seed, dbt snapshot, or dbt test.
- on-run-end: executed at the end of dbt build, dbt compile, dbt docs generate, dbt run, dbt seed, dbt snapshot, or dbt test.
This blogpost is a blogpost in a serie of blogposts :
- Build a data warehouse with DBT and Snowflake on AdventureWorksLT (PART I)
- Build Staging and Dimensions in DBT for Snowflake (PART II)
- Sources in DBT for Snowflake (PART III)
- Data freshness for DBT in snowflake (Part IV)
- Snapshots in DBT for Snowflake (Part V)
- Generic tests in DBT for Snowflake (PART VI)
- Singular tests in DBT for Snowflake (Part VII)
- Add packages to your DBT project (Part VIII)
- Adding documentation to your DBT project (Part IX)
- Working with hooks in DBT (Part X).
Hooks
--Auditing
CREATE TABLE IF NOT EXISTS RUN (
RUN_ID INT AUTOINCREMENT START 1 INCREMENT 1,
RUN_STARTDATE TIMESTAMP_NTZ,
RUN_ENDDATE TIMESTAMP_NTZ
);
CREATE TABLE IF NOT EXISTS MESSAGE (
MESSAGE_ID INT autoincrement start 1 increment 1,
RUN_ID INT, -- Runnumber of the complete run
MESSAGE_STATUS STRING, -- START, END, ERROR, INTERMEDIATE
MESSAGE_DESCRIPTION STRING, -- Logging message or error message
MESSAGE_LOCATION STRING, -- Individual Stored procedurename
MESSAGE_LAYER STRING, -- Database layer : DATAVAULT, DATAMART
MESSAGE_AREA STRING, -- Subject Area : LEGACY, FINANCE, etc
MESSAGE_LEVEL NUMBER, -- Stored procedure level : 1 = MASTER, 50 = DATAVAULT or DATAMART, 100 = Low level stored procedure
MESSAGE_DATE TIMESTAMP_NTZ, -- Date of logging
MESSAGE_ROWCNT NUMBER -- Affected rows of SQL executed
);Now, I'm not rebuilding the complete logic into DBT, but I will take some key elements of the logging and build that into DBT.
on-run-start: "INSERT INTO RUN (RUN_STARTDATE) SELECT CURRENT_TIMESTAMP();"
on-run-end: "INSERT INTO RUN (RUN_STARTDATE) SELECT CURRENT_TIMESTAMP();"And then run the following command in the project folder :
dbt run -m Dim_CustomerResulting in the following :
How does it look in Snowflake when the command has been executed?
Now the lets check the other hooks in DBT : pre-hook and post-hook. Here I added some code in the dbt_project.yml file : "INSERT INTO MESSAGE table".
dbt run -m Dim_CustomerFinal thoughts
donderdag 28 december 2023
Adding documentation to your DBT project (Part IX)
Introduction
Sometimes you get the question from a collegue about that he or she wants to know more about how a specific measure is generated. DBT has a documentation option you can use for this. Lets try this and I'll show this in this blogpost.
This blogpost is a blogpost in a serie of blogposts :
- Build a data warehouse with DBT and Snowflake on AdventureWorksLT (PART I)
- Build Staging and Dimensions in DBT for Snowflake (PART II)
- Sources in DBT for Snowflake (PART III)
- Data freshness for DBT in snowflake (Part IV)
- Snapshots in DBT for Snowflake (Part V)
- Generic tests in DBT for Snowflake (PART VI)
- Singular tests in DBT for Snowflake (Part VII)
- Add packages to your DBT project (Part VIII)
- Adding documentation to your DBT project (Part IX)
- Working with hooks in DBT (Part X)
- Ephemeral tables in DBT (Part XI)
Documentation
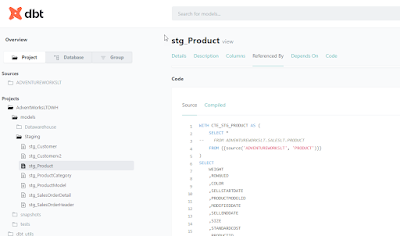
There are two important commands for documentation : generate and serve. Lets find out more about them. For using the documentation, you can add a description tag to your YAML files.
and here..
And then use the command dbt docs generate :
The next command is to use dbt docs serve :
And this will open a html page on your local machine :
All kind of information is available in the documentation. It's truly amazing.
Final thoughts
This is an amazing feature of DBT! You can easily generate the documentation with dbt docs
Hennie